3. Algorithmes de recherche dans les systèmes à agents
3.3. Le problème de la satisfaction des contraintes (PSC)

3.3.3. L`algorithme de recherche par engagement minimum (REM)

Il se ressemble à l'algorithme précédent avec les différences suivantes

• la priorité de chaque agent peut se modifier durant l`exécution de l`algorithme;
• chaque agent envoie sa valeur vers tous les nœuds avec lesquels il est lié par un arc de contrainte, quelle que soit la priorité (dans l'algorithme Retour en arrière asynchrone, la valeur courante était transmise seulement par les nœuds ayant une priorité inférieure à celle du nœud émetteur)
• les messages de type “correcte_?” communiquent la valeur courante ainsi que la priorité du nœud émetteur ;
• - si un agent ne peut pas obtenir la consistance (il y a des contraintes non satisfaites avec des variables de priorités plus grandes), alors il va choisir pour sa variable propre la valeur qui minimise le nombre de contraintes non satisfaites avec les agents de priorité plus faible
• si on ne trouve aucune valeur consistante avec la liste état_des_voisins, l`agent incréments sa priorité (+1).

Le processus de traitement des messages peut être représenté par le pseudo code suivant.

Procédure Réception_correcte_?_ (x_j, d_j, priorité) est

// La procédure est appelée à l`arrivée d`un message
// de type “correcte_?” émis par le nœud x_j qui transmet
// sa nouvelle valeur d_j et sa priorité au nœud courant (x_i)
// qui a un rôle d'évaluateur de contrainte
//

  Insert (état_des_voisins, (x_j, d_j , priorité) )
  Vérifie_état_des_voisins()

Fin

La procédure Réception_incorrect_ (x_j , E) est

// La procédure est appelée à l`arrivée d`un message
// de type incorrect émis par le nœud x_j qui a un rôle
// d`évaluateur de contrainte pour le nœud courant (x_i)
// E = {(x_k, d_k, p_k)/ d_k est une valeur incorrecte pour le nœud x_k
//                   p_k est la priorité de x_k }

     pour *) "(x_k, d_k)ÎE faire
          Insert ( valeurs_refusées, (x_k, d_k , p_k ) )
          si *) le nœud (x_k) n`est pas voisin du nœud courant (x_i) alors
               *) insérer le nœud (x_k) dans la liste des voisins de (x_i)
                Insert (état_des_voisins, (x_k, d_k, p_k) )
          fin si
      fin pour
     Vérifie_état_des_voisins()
Fin

Procédure Vérifie_état_des_voisins() est

     si *)la valeur_courante n`est pas consistante avec la liste état_des_voisins  alors
          si *)aucune valeur de D<sub>i</sub> n`est consistante  avec la liste état_des_voisins alors
               RetourEnArrière()
          sinon
               valeur_courante = Choix_valeur_consistante_Min (D_i , état_des_voisins)
               pour *) "(x_j) Î voisins(x_i) faire
                    Envoyer (“correcte_?”, x_j, (x_i , valeur_courante, priorité_courante ))
               fin pour
           fin si
      fin si
Fin

Procédure RetourEnArrière() est

     F = { A / A un sous-ensemble inconsistant qui se trouve dans l`état_des_voisins }
     si F = f alors
          *) émet des messages aux autres agents en annonçant qu`il n`existe pas de solution
          *) termine l`algorithme
     fin si
     pour *) "A Î F non-envoyé par x_i jusqu`à ce moment faire
          Insert (incorrecte_envoyés, A)
          pour *) "(x_j, d_j, p_j) Î A faire
               Envoyer (incorrect, x_j, (x_i , A))
          fin pour
      fin pour

     pmax = max ({p_j / (x_j, d_j, p_j) Î état_des_voisins })
     priorité_courante = pmax + 1
     valeur_courante = Choix_valeur_consistante_Min (D_i , état_des_voisins)
     pour *) "(x_j) Î voisins(x_i) faire
          Envoyer (“correcte_?”, x_j, (x_i , valeur_courante,  priorité_courante))
     fin pour
Fin

La fonction Choix_valeur_consistante_Min (D_i , état_des_voisins) cherche une valeur consistante avec les contraintes où sont impliquées les variables qui se trouvent dans les nœuds de priorité plus grande que le nœud courant et qui minimisent le nombre de contraintes non satisfaites avec les variables des agents de priorité plus petite.

Analyse de l`algorithme R.E.M.
Complétude – l`algorithme est complet ;
Complexité en temps – exponentielle dans le nombre des variables, n ;
Complexité en espace – exponentielle en n ;

Pour montrer que l`algorithme est complet il faut observer qu`à un certain moment les priorités ne se modifient plus. Si les priorités sont stables alors

• il n'existe pas d'agents avec des variables qui ne satisfont pas les contraintes
• il n`existe pas de cycles infinis par la transmission répétée de messages.

L`algorithme s `arrêtera en temps fini s`il a trouvé une solution où s`il n`y a pas de solution.

Question. Comment peut-on justifier l`affirmation que les priorités deviennent stables à un certain moment ?

Cliquez ici pour voir la réponse

Exemple. On considère le problème de la disposition des reines sur un échiquier de 4x4. L`état initial est présenté figure 3.3.7. Les positions des reines sont données par les valeurs courantes des quatre agents x₁, x₂, x₃, x₄  qui ont initialement des priorités nulles.

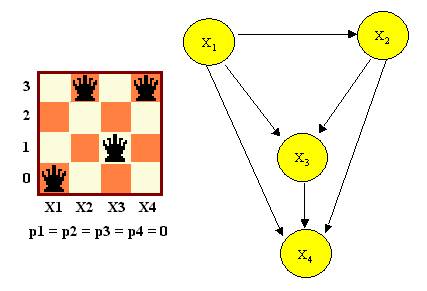
Figure 3.3.7. L`état initial du système à agents pour la résolution du problème à 4 reines

Dans l`état initial seulement la valeur courante de l`agent x₄  n`est pas consistante. Ensuite le processus se déroule conformément à la description qui suit.

L`agent x₄

• exécute la procédure RetourEnArrière() et envoie des messages de type incorrect aux agents x₁ et x₂
• sa priorité devient 1 (pmax=0)
• valeur_courante =  Choix_valeur_consistante_Min([0,3],état_des_voisins) (la seule valeur possible est 2, qui ne respecte qu`une seule contrainte – avec l`agent x₃)
• communique aux voisins, par messages de type “correcte_?”, sa nouvelle valeur courante et sa priorité.

Les agents x₁ et  x₂

• reçoivent le message de type incorrect et celui de type “correcte_?” émis par l`agent x<sub>4</sub>;
  • on suppose que le deuxième message est arrivé suffisamment vite pour que la procédure Vérifie_état_des_voisins() soit démarrée après l`arrivée du message de type “correcte_?”; en ce cas la procédure observe que les valeurs courantes sont consistantes.

Remarque. Après la réception  du message de type incorrect l`activité de ces deux agents peut se dérouler simultanément avec l`activité de l`agent x₄

L`agent x₃

• reçoit le message de type “correcte_?” émis par l`agent x<sub>4</sub> et constate que sa valeur courante ne vérifie pas une contrainte avec un agent plus prioritaire (x<sub>4</sub>)
  • on appelle la procédure RetourEnArrière() et envoie un message de type incorrect à l`agent x₄
  • sa priorité devient 2 (pmax=1, la priorité de x₄); parce que l`agent x₄ a communiqué par un message de type “correcte_?”, sa nouvelle priorité, la détermination de pmax est locale et ne nécessite pas d'autres ressources de communication
  • valeur_courante =  Choix_valeur_consistante_Min([0,3],état_des_voisins) (deux valeurs sont possibles, 0 et 1, qui minimisent le nombre de contraintes non satisfaites avec les agents x₁,x₂ et x₄: on suppose que la valeur 0 est sélectée)
  • communique aux voisins, par messages de type “correcte_?”, sa nouvelle valeur courante et sa priorité

L`agent x₄

• reçoit le message de type incorrect et celui de type "correcte_?" émis par l'agent x3; leur arrivée est supposée séparée par un très petit délai, de sorte que l'effet du premier message est annulé par le deuxième.

L`agent x₁

• reçoit le message de type incorrect et celui de type “correcte_?” émis par l`agent x₃;
  • exécute la procédure Vérifie_état_des_voisins()et modifie sa valeur à 1; on a alors trouvé une solution du problème

Remarque. Il n`est pas obligatoire que le fonctionnement du réseau de communication et la procédure de sélection Choix_valeur_consistante_Min() soient identiques dans tous les cas. Il peut exister des différences entre les successions des événements, mais l`algorithme se terminera avec le même résultat.

Question. La complexité exponentielle en espace mémoire peut engendrer des problèmes aux systèmes avec beaucoup d'agents. Comment croyez-vous qu'on peut lever cet obstacle ?

Cliquez ici pour voir la réponse