Real-Time Search
Notes due to – Brian Roberts,
grad. student at CS Dept., WPI
MAS Course
Introduction
To search, according to Merriam-Webster's online
dictionary, means “to look into or over carefully or thoroughly in an effort
to find or discover something: as to examine in seeking something; to make
painstaking investigation or examination.” These definitions accurately
describe the term, as used in the multi-agents systems field. An agent,
in an initial state or position, must carefully investigate possible options,
in order to find a path to a final goal or solution.
Although there are many different algorithms
available, these can be categorized into two main classes: off-line and
real-time. An off-line search finds a complete solution path before attempting
any steps towards the goal. In contrast, a real-time search computes just
enough, so as to determine a reasonable next step. After taking the previous
'most reasonable' move, a real-time search algorithm performs further computation
to determine the next 'most reasonable' step...and so on, repeating until
a final state or goal is reached. Real-time searches do not guarantee to
find an optimal solution, but serve only to interleave planning steps and
actually executing them.
Put simply, these searches do what is known as
'path-finding'. This is used when an agent needs to get from one state
to a (possibly) distant state through a sequence of operators or moves.
A path-finding problem, MAS and other areas, consists of the following
components:
?N:
a set of nodes, each representing a state,
?L:
set of directed links, each representing an operator available to a problem-solving
agent.
?s:
a unique node, representing the start node
?G:
set of nodes G, each representing
a final state (G ? N)
Every directed link, l,
has an associated weight or distance, which represents the cost to the
agent of applying the operator. Nodes which can be reached directed from
a node i, are called the neighbors
of node i.
The basis of the algorithms mentioned above,
and later in this text, is asynchronous
dynamic programming. This process relies on the principle
of optimality:a
path P is optimal if, and only if all sub-paths along the path are optimal.
That is, for every intermediate path between the starting and ending node,
the path must be the shortest possible available.
For convenience,
h*(i)
is used to denote the distance from node i
to the nearest goal node. Asynchronous dynamic programming
repeatedly computes successive approximations of h*(i),
denoted by h(i), at
each node in the graph. For true asynchronous dynamic programming, every
node must contain an asynchronous process, independently updating its h(i)
approximation function. Each node i
follows the following algorithm:
Compute
for each neighbor node j:
f*(j) = k(i, j) + h(j)
Where:
k(i,
j): distance from node i to j
h(i):
estimated shortest distance from node i to goal
Update
h(i) = minj f(j)
This
process is repeated until the approximations h(i)
convert to the actual values of h*(i).
It can be proved that h(i)
will converge for every node i,
provided that k(i, j)
never over-estimates the cost.
Algorithms
A*
No paper would be complete without mentioning
A* (pronounced: “A star”), perhaps the most famous heuristic off-line
searching algorithm of all-time. Several real-time algorithms have been
based off of A*, including
the Learning Real-Time A* and Real-time A* algorithms.
The basic concept of the A* algorithm is a best-first
search—the most probable paths are explored first, searching outward from
the starting node until it reaches the goal node . The best path is determined
by choosing the option with the lowest cost, where cost is measured by
the function: f(n) = g(n) + h'(n).
The function g(n) is the actual cost of the path so far, while h'(n)
is a heuristic function of the estimated cost of the path from the current
state to the final goal.
This algorithm will always find an optimal path
to a goal, provided the heuristic function is 'admissible'—it does not
over-estimate the cost from the current node to the goal. It is worthy
to note, that if the heuristic function too often under-estimates the costs,
then A* will have to search too many probable paths, and may run out of
time before any solution is found. However, if the heuristic function too
often over-estimates the costs, a solution can be found very quickly, but
will likely be sub-optimal. The admissibility of h'(n)
is
error-tolerant—should h'(n) occasionally over-estimates h
of the path by cost C, then A* will only occasionally find an answer
that costs more than cost C more than the optimal cost.
Learning Real-Time A*
The algorithm Learning
Real-Time A* (LRTA*) is conceptionally
almost the same as A*; LRTA* can be viewed as the real-time version of
A*. The traversal through the nodes is as follows:
for
each neighbor j of
current node i
compute f(j)
= k(i,j) + h(j)
store
the new h(i) = minj f(i)
move
to the node j with min
f(j)
Ties for minimal
f(j) values are broken randomly. LTRA* 'learns' the optimal path
via repeated trails. As long as initial h(i)
values are not over-stated, this algorithms is guaranteed to find a solution.
Over repeated trials, LTRA* will find the most optimal solution. It should
be noted, that using the proper heuristic estimation function will speed
up finding the optimal solution. A simple example of the difference good
heuristics can make can be observed in the 8-puzzle game. The 8-puzzle consists
of 8 numbered, movable tiles, in a 3x3 frame. One of the cells of the frame
is empty, which makes it possible to move the tiles. The object of the
puzzle is to transform one configuration of the tiles into another. Two
well-known heuristic estimation functions for this problem are: the number
of misplaced tiles, and the sum total of the Manhattan distances of misplaced
tiles.
The first function is easily understood: if x
tiles are incorrectly placed, then the estimation function h(i)
would return x. The second formula is only slightly harder to grasp.
A Manhattan distance measurement is equated by summing the horizontal
and vertical distances of each tile from its goal position. Thus, if the
tiles are currently in the following position:
Current state
And the goal is to
arrange the tile in this manner:
Goal State
Then, since the '1' tile is in the correct position,
its Manhattan distance is 0. The '2' is shifted 1 position horizontally
and 2 positions vertically from its goal position, adding up to a distance
of 3.
|
Distance |
| Tile |
Horizontal |
Vertical |
Manhattan |
|
1
|
0
|
0
|
0
|
|
2
|
1
|
2
|
3
|
|
3
|
1
|
1
|
2
|
|
4
|
2
|
1
|
3
|
|
5
|
0
|
1
|
1
|
|
6
|
1
|
1
|
2
|
|
7
|
2
|
0
|
2
|
|
8
|
1
|
1
|
2
|
| |
|
|
|
|
Total
|
8
|
7
|
15
|
By counting
the number of non-zero manhattan distances, we arrive at the number of
misplaced tiles in this example: 8.
A good heuristic function should estimate the
cost of moving from the current state to the goal state, as accurately
as possible, but without over estimating the distance. Since every tile
must be moved individually, the Manhattan displacement of a tile will never
exceed the number of moves required to move it into its correct position.
The total cost of moving all the tiles into their correct positions can
never exceed the sum total Manhattan distance. The misplaced tiles metric
can be calculated by counting the number of non-zero Manhattan numbers,
and therefore will never be greater than the Manhattan distance. From the
above, we derive the following relationships:
misplaced_tiles(i) ? manhattan(i) ? h(i)
This clearly
shows that the Manhattan distance is a better estimation to use as a heuristic
function.
Real-Time A*
Real-Time A*(RTA*),
is exactly the same as LRTA*, which one exception. When the new value of
h(i) is stored, it is updated with the second least value. So, the
algorithm for RTA* reads:
for
each neighbor j of
current node i
compute f(j)
= k(i,j) + h(j)
store
the new h(i) = secondminj f(j)
move
to the node j with min
f(j)
The key difference
between RTA* and LRTA* (updating h(i) withsecondminj
f(j) versusminj
f(j)) allows an agent using the RTA*
to make locally-optimal decisions on tree structures. That is, the path
toward the goal chosen by RTA* has the minimum estimated cost based on
the already-obtained information. Although this allows RTA* to overestimate
heuristic costs, RTA* learn more efficiently on a single trial, and will
usually arrive at the goal quicker. If a problem is to be solved repeatedly
with the same goal state but different initial states, LRTA* will improve
its performance over time, and eventually converge on the optimal solutions
to along all paths.
Moving Target Search
Moving Target
Search (MTS) allows one to relax the assumption that the goal location
remains stationary. This allows the target to move while the search is
in progress. The goal is reached when both the solver and the target are
standing on the same node in the graph.
Several variables
are used in this search algorithm: xi is the current position of the problem
solver, xj is neighbor positions of problem solver, yi is the current position
of target, and yj is the neighbor positions of target.
The algorithm has
two parts, one part to be executed when the problem solver moves, the other
to be executed when the target moves.
When problem solver
moves
For each neighbor
xj
calculate h(xj, yi)
Update h(xi, yi) = max (h(xi, yi), minx'j h(x'j,
yi + 1)
Move to xj where min h(xj, yj) and update xi
When target moves:
Calculate h(xi, yj)
for target's new yj
h(xi, yi) = max (h(xi, yi), h(xi, yj) – 1)
Update position yi = yj
Real-Time Bidirectional Search
Real-time
Bidirectional Search (RTBS) involves
two agents simultaneously searching is the same environment. There are
two types of RTBS: centralized and decoupled. In centralized RTBS, agents
coordinate their actions for mutual benefit. In decoupled RTBS, each agent
chooses its actions independently. One agent maybe even works against the
other agent, albeit unintentionally. The algorithm is fairly
simple, because it must use another, previous algorithm for the actual
searching.
Repeated execute following:
Control step: select forward or backwards
move
Forward move:
Problem solver from initial state moves towards second, 'target' agent.
Backwards
move: Solver from goal state moves towards first agent.
In
Centralized RTBS, one algorithm to
use is LRTA*/B, a bidirectional version of LRTA*. The algorithm is described
as follows (adapted from [4], with modifications to allows costs > 1):
LRTA*/B
Control Strategy:
Calculate h(x',
y) for each neighbor x'
of x.
Calculate h(x, y')
for each neighbor y' of y.
Update
the value of h(x, y) as follows:
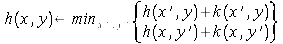
If minx'
h(x', y) < miny' h(x, y'), select a
forward move.
If minx'
h(x', y) > miny' h(x, y'), select a backward
move.
Otherwise, select a forward or backward move
randomly.
Forward move:
Move the forward
problem solver to the neighbor x'
with the minimum h(x', y),
i.e., assign the value of x'
to x. (Ties are broken
randomly.)
Backward move:
Move the backward
problem solver to the neighbor x'
with the minimum h(x, y'),
i.e., assign the value of y'
to y. (Ties are broken
randomly.)
Similarly,
the RTA* algorithm may be adopted for bidirectional search, resulting in
the RTA*/B algorithm.
This
strategy calculates all possible forward and backward moves, and selects
the best choice. Both solvers are completely controlled by the centralized
decision-maker. The control strategy of LRTA*/B clearly shows
the coordination of the two agents: the solver whose h(x, y)
distance estimation for reaching the other agent is smaller is allowed
to move. Since the move with the smaller cost total is always taken, LRTA*/B
will take the shortest path which can be found with LTRA*.
In
Decoupled
RTBS, agents do not coordinate their
moves, but independently seek to meet with the other agent. The only search
algorithm which can handle this independence is the MTS algorithm. Ishida
describes a bidirectional MTS, called MTS/B in [4]. The bidirectional MTS/B
differs from the unidirectional MTS mainly in the fact that both agents
are actively seeking to rendezvous with the other agent.
In
the decoupled control strategy, the algorithm “employs the minimal control
necessary to ensure the termination of the algorithm” [1]. This
results in both problem solvers independently making all decisions. The
algorithm described in both [1] and [4] simply select forward and backward
moves alternately.
One
surprising constraint of MTS/B is that the problem solver must move faster
than the target. This assumption was originally introduced in the description
of MTS, when the target was trying to avoid the problem solver. This assumption
must remain in order to prevent the agents from infinitely looping. With
out this assumption, infinite looping could occur when agents are on opposites
sides of an obstacle. If each agent attempts to move around the obstacle,
but end up either continually chasing each other around the obstacle, or
shuffling back and forth from side to side on opposite ends of the barrier.
In
addition to classifying RTBS algorithms into decoupled- and centralized-control,
each algorithm can be further sub-divided along the lines of how much information
is shared between agents. Agents can either share heuristic information
or maintain and update their own h(x, y) values. These classifications
are called: shared heuristic information
anddistributed heuristic information
schemes. MTS/B is a distributed heuristic decoupled-control RTBS algorithm,
while LRTA*/B is a shared heuristic centralized-controlRTBS algorithm.
The
performance of both decoupled- and centralized control RTBS algorithms
has been compared [1 and 4] against each other. When heuristic functions
can be relied on to supply accurate values, the decoupled algorithm performed
better. While the number of moves needed by the agents to rendezvous were
approximately the same, the decoupled RTBS must only expand half as many
states as the centralized version. This means that decisions can be made
independently by the two problem solvers without losing efficiency, while
halving the planning time needed. In uncertain situations,
when the heuristic function cannot be relied upon to supply accurate values:
the centralized strategy works best. The number of moves required by the
centralized RTBS algorithm was approximately one-half that of its decoupled
counterpart.
The
performance of both RTBS algorithms was also compared to Real-time Unidirectional
Search (RTUS). When the heuristic function is accurate, the difference
in number of moves required in decoupled-RTBS, centralized-RTBS and RTUS
is negligible. This is because, in clear situations, various search techniques
can be used do obtain near optimal solutions. In uncertain situations,
clear differences were observed, but can be generally applied. The comparison
of RTBS to RTUS is highly reliant on the problem type. For n-puzzles, RTBS
is clearly a better choice, reducing the number of moves over RTUS by a
factor of 2 for 15-puzzles, and by 6 for 24-puzzles. However, in randomly
generated mazes, RTUS becomes increasing better as the obstacle-ratio increases.
Summary
Modern
search algorithms are based on asynchronous dynamic programming and can
be categorized into two categories: off-line and real-time. Real-time is
used when movement steps must be interleaved with planning steps.
Many
different algorithms for searching have been proposed, the most often used
algorithms include: A*, Learning Real-Time A* (LRTA*), Real-Time A* (RTA*),
and Moving Target Search (MTS). A* is an often used off-line algorithm.
LRTA* is a real-time version of A*. RTA* differs from LRTA* only in updating
its heuristic values. MTS allows the problem solver to seek a target that
moves.
Bidirectional
search is when 2 agents want to rendezvous. Real-Time Bidirectional Search
(RTBS) is categorized into two different levels coordination: decoupled
and centralized. The information sharing can also be classified into: distributed
or shared. LTRA*/B is centralized and shared, while MTS/B is decoupled
and distributed.
Bidirectional
search works similarly to unidirectional when heuristic functions are accurate,
but often differ when distances are uncertain. Bidirectional works better
for n-puzzle problems, unidirectional for mazes with a high (>20%) obstacle-density.
References
Real-time
bidirectional search: Coordinated problem solving in uncertain situations.
T. Ishida, IEEE Trans. on PAMI, Vol.18, No.6, 1996, p.617-627.
Moving-Target
Search: A Real-Time Search for Changing Goals. T. Ishida. and R. Korf.
IEEE Trans. on PAMI, Vol.17, No.6, 1995, p.609-619.
The
Trailblazer Search: A New Method for Searching and Capturing Moving Targets.
T. Sasaki, et al. AAAI-94, pp. 1,347-1,352. 1994
Two
is not Always Better than One: Experiences in Real-Time Bidirectional Search.
T. Ishida. Int'l Conf. Multi-Agent Systems (ICMAS-95, pp. 185-192. 1995
Multi-Agent
Systems: A Modern Approach to Distributed Artificial Intelligence.
G. Weiss (ed). MIT Press, 2001. Chapter 4, pp. 165-199.
![]()