3. Algorithmes de recherche dans les systèmes à agents
3.1. Recherche de la solution du problème

3.1.1. Notions préliminaires

Plusieurs recherches en IA se sont concentrées sur la résolution des problèmes. Parmi les diverses approches, les algorithmes de recherche de la solution fournissent des mécanismes de résolution généraux et efficaces.

Pour formaliser la résolution par recherche d`un problème on utilisera les notions suivantes: 

• l`état initial ou le point de départ dans le processus de recherche
• l`ensemble d`opérateurs (actions) qui permettent les transitions d`un état à l`autre
• l`état solution – le but de la recherche

L`espace d`états constitue une abstraction du monde réel. L`espace d`états peut être  décrit par l`état initial et l`ensemble des opérateurs. Une suite d`états produits par l`application valide des opérateurs forme un chemin dans l`espace d`états. Il peut être observé qu`un chemin est décrit aussi par l`état initial et la séquence des opérateurs qui a produit la suite d`états.

Le processus de recherche se finalise par l`identification d`un chemin qui part de l`état initial et arrive dans l`état solution. Pour tester si un état quelconque est un état solution on a besoin d`une fonction appelée fonction test-but.

Il peut arriver que plusieurs chemins se terminent avec l'état solution. Il est utile dans ce cas d'avoir un critère de performance afin de décider quel est le meilleur chemin. Une telle fonction s'appelle fonction coût-chemin.

Une solution est un chemin menant à l`état solution. Plus concrètement, une solution sera une suite d'opérateurs qui étant appliqués successivement, en partant de l`état initial, conduit à l`état solution.

Exemple. On considère le problème des Tours de Hanoi avec trois tours. On demande de déplacer les disques situés sur la première tour sur une autre, de façon qu`un disque repose toujours sur un autre disque de taille supérieure ou sur une tour libre.

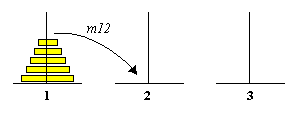
Figure 3.1.1. Le problème des Tours de Hanoi

Un état sera décrit par le triplet (A,B,C) où A,B,C sont les ensembles de disques situés sur les trois tours.  Si on considère un cas particulier avec deux disques sur la première tour l`état initial est E<sub>0</sub> = ( {1,2},Ø,Ø ) où 1 et 2 représentent respectivement le disque de petite taille et le disque de taille supérieure. Parce qu`on n`a pas spécifié la tour où reposeront à la fin les disques il y a deux états solution : E_f2 = (Ø, {1,2}, Ø) et E_f3= (Ø, Ø, {1,2}).

L`ensemble d `opérateurs est M = { m_ij / i=1,3 , j=1,3}, où m_ij signifie le déplacement du plus petit disque situé au sommet de la tour i sur la tour j (voir la figure 3.1.1). Mais tous les opérateurs peuvent être appliqués à tous états. On observe que si on est en E0 seuls les opérateurs m₁₂ et m₁₃ peuvent être appliqués. Les opérateurs admettent des inverses. Si on applique l`opérateur m<sub>12</sub> dans l`état E₀, on exécute une transition vers E₁ = ({2}, {1}, Ø), d`où si on applique m₂₁ on revient de nouveau en E₀.

L`espace d`états est décrit par la couple (E₀, M). Les solutions optimales sont (E₀, m₁₃, m₁₂, m₃₂) pour atteindre E_f2 et (E₀, m₁₂, m₁₃, m₂₃) pour obtenir E_f3.

Question. Quelles sont les autres solutions possibles obtenues après l'application de 5 opérateurs (les longueurs des chemins sont 5) ?

Cliquer ici pour voir la réponse.

Pour pouvoir résoudre un problème, un algorithme de recherche doit réaliser une exploration de l`espace d`états d`une manière systématique et contrôlée.

On distingue deux classes d'algorithmes de recherche :

1. algorithmes non-informés ou `aveugles` (brute force), qui réalisent une recherche exhaustive, sans utiliser aucune information concernant la structure de l`espace d`états pour optimiser la recherche;
2. algorithmes informés ou heuristiques qui utilisent des sources d`information supplémentaires ces algorithmes parviennent ainsi à des performances meilleures.

Les critères suivants sont utilisés pour apprécier les performances des algorithmes de recherche

• optimalité – c'est la caractéristique d`un algorithme de recherche qui trouve la meilleure solution (pour un problème qui en admet plusieurs)
• complétude – si une solution existe l`algorithme garantit qu`elle sera trouvée
• complexité en temps – estimation du temps nécessaire pour résoudre un problème,
• complexité en espace – estimation de l`espace mémoire nécessaire à l`algorithme pour résoudre le problème.

Les deux complexités, en temps et en espace, sont exprimées comme des fonctions de la dimension du problème.