3. Algorithmes de recherche dans les systèmes à agents
3.1. Recherche de la solution du problème

3.1.2. Algorithme général de recherche

L`espace d`états d`un problème se peut représenter comme un graphe orienté crée en partant du nœud représentant l`état initial et en appliquant les opérateurs qui modélisent l`ensemble des actions du monde réel. Il faut souligner qu`il n`est pas nécessaire d`avoir mémoriser ce graphe. Il peut être construit lors de la recherche de la solution.

Exemple. Dans le problème des Tours de Hanoï avec l`état initial décrit par ({1,2}, Ø, Ø) le graphe représentant l`espace d`états est présenté dans la figure 3.1.2.

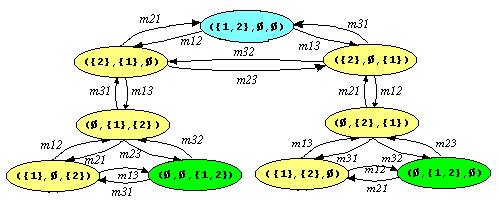
Figure 3.1.2. Le graphe du problème des Tours de Hanoï avec 2 disques et 3 tours

L`algorithme général de recherche réalise une exploration simulée d`un espace d`états, construit au fur et à mesure de la recherche, processus appelé expansion d`états. Pendant la recherche on étend les états successeurs des états explorés, en partant de l`état initial, jusqu`où on arrive dans un état solution.

L`algorithme peut être exprimé par le pseudo code suivant

Fonction RechercheGénéral (étatInitial, ensemble_opérateurs) est
 S = ConstruireVide()
 Insérer (S, Nœud(étatInitial))
tant que non Vide(S)  faire
   NœudCourant = Extraire (S)
   if Test_But(NœudCourant)=vrai 
   alors
     Détruire (S)
     retourne NœudCourant
   sinon
     pour *) chacune op dans ensemble_opérateurs faire
        x = Successeur(NœudCourant, op)
        si Valide(x) alors Insérer(S, x) fin si
     fin pour
   fin si
 fin tant que
 Détruire (S)
 retourne vide
Fin

Cet algorithme utilise une structure de données, S, qui est construite vide au début et détruite à la fin. Le type abstrait de donnée (TAD) de cette structure est défini par les fonctions:

• Insérer (S, x) – introduit l`élément x dans la structure S
• Extraire (S) – fournit l`élément qui se trouve “en face” de la structure S et l`élimine aussi
• Vide(S) – fonction booléenne qui retourne vrai si la structure S est vide

On observe que les arguments de la fonction RechercheGénéral() représentent l`espace d`états du problème. Les autres fonctions utilisées dans l`algorithme sont des fonctions spécifiques à l`abstraction du problème.

• Test_But(NœudCourant) - fonction booléenne qui retourne vrai si le NœudCourant représente l`état solution ;
• Successeur(NœudCourant, op) – fonction qui retourne le nœud successeur du NœudCourant obtenu suite à l`application de l`opérateur op; si l`opérateur op ne peut pas être appliqué au NœudCourant alors la fonction retournera nul
• Valide(x) - fonction booléenne qui retourne vrai si x n`est pas nul et si x est un nœud qui peut être inséré dans la structure S.

Les nœuds qui sont manipulés par cet algorithme représentent aussi des données structurées. Par exemple on a vu dans l`exemple des Tours de Hanoï qu`un état est représenté par un triplet.

Complétude

Cet algorithme s`avère complet pour les espaces d`états finis et acycliques. Pour maintenir la complétude de l`algorithme dans le cas des espaces finis, mais qui contiennent des cycles, il faut avoir un mécanisme qui garantit que tous les nœuds ne sont visités qu`une seule fois durant les traitements de l`algorithme. Cette tâche sera effectuée aussi par la fonction Valide(x). 

C`est le type abstrait de donnée (TAD) utilisé pour la structure S qui déterminera le parcours dans l`espace d`états du problème et en conséquence l`algorithme particulier de recherche.