3. Algorithmes de recherche dans les systèmes à agents
3.4. Stratégies en jeux

3.4.1. Jeux et recherche

Les algorithmes pour les stratégies en jeux à deux joueurs représentent un domaine très attractif en Intelligence Artificielle en raison du défi intellectuel et de la possibilité de commencer rapidement une recherche grâce à la faible quantité de connaissances nécessaires pour jouer.

La présence d'un adversaire apporte un tel dégré d'imprévu et la complexité des jeux est si grande (e.g. dans le jeu d'échec on a 35 !) que les solutions pour les programmes de jeux ne sont pas du tout faciles à trouver. On peut observer aussi que pour les jeux complexes comme le jeu d'échec ou GO, on ne peut pas explorer l'espace d'états en son intégralité pour rechercher à chaque pas le coup qui va apporter la victoire.

Un programme de jeux comprend un générateur de coups, une fonction de gain pour évaluer la qualité des coups, similaire à la fonction test-but dont on a parlé dans la section 3.1, pour déterminer la fin de jeu et une stratégie de contrôle qui permet de choisir le coup qui va apporter le plus de bénéfices.

Le but est de réaliser des agents capables de jouer avec d'autres agents et de réussir à gagner la partie.

Pour formaliser le processus de recherche du meilleur coup on utilise un arbre de décision appelé Arbre de Jeu, qui est construit pour chaque position p comme suit:

• la position p constitue la racine de l`arbre.
• si les coups possibles à partir de la position p, donnent les positions p1,..., pn, alors p a comme fils p1,..., pn.
• les nœuds correspondant aux positions finales sont les feuilles de l`arbre de jeu

On va supposer que les deux joueurs exécutent alternativement un seul coup. Pour cette catégorie de jeux, les niveaux des nœuds pour les agents adversaires s'alternent dans l'arbre de jeu. On va remarquer aussi qu'un arbre qui a comme racine la position initiale du jeu contient toutes les parties possibles qui commencent par cette position.

Les algorithmes de jeux sont basés sur la construction de cet arbre de façon que l'agent puisse choisir le meilleur coup à partir d'une position p. Mais, même si l'arbre de jeu est fini sa dimension peut dépasser les possibilités du mémoire de notre agent. Il est plus raisonnable de le construire partiellement, à chaque position courante, en utilisant les règles du jeu.

Notre agent, qu'on désire munir d'un logiciel de jeu, doit choisir son coup parmi l'ensemble fini des coups qui peuvent avancer le jeu de la position courante p vers une des positions p1,...,pn. Pour faire le choix il faut déterminer la plus grande valeur de f(p1), ..., f(pn), où f() est la fonction d'évaluation statique.

Pour le calcule de cette fonction il existe plusieurs stratégies. En général, pour calculer les valeurs f(pi) on va commencer avec les nœuds fils qi de sous arbre dont la racine est p_i. Par exemple on va associe à f(qi) la valeur +100 si dans le nœud qi la partie se termine par une victoire, -100 pour une défaite et 0 pour une partie nulle. À partir de ces valeurs assignées aux nœuds qi terminaux l'algorithme déterminera les valeurs du père de qi (le niveau au-dessus de qi) et ensuite, en remontant vers la racine, pour les parents des parents et à la fin on obtiendra la valeur de f(pi).

On peut observer l`association des valeurs –100, 0 et +100 aux nœuds terminaux dans la figure 3.4.1 qui représente une partie de l`arbre de jeu pour le jeu de Tic Tac Toe. On remarque que la racine est l`état initial du jeu, avec toutes les cases vides. On suppose que le joueur X va commencer la partie, donc ce niveau est le niveau de décision pour X (coloré en jaune).

Les 9 fils de la racine sont les 9 positions possibles pour le joueur X. Le niveau suivant est le niveau de décision pour le joueur O (coloré en bleu) parce que c'est au tour du joueur O de choisir un coup. Les positions possibles pour le joueur O sont au nombre de 9 x 8 =72 et ne sont pas toutes représentées sur la figure.

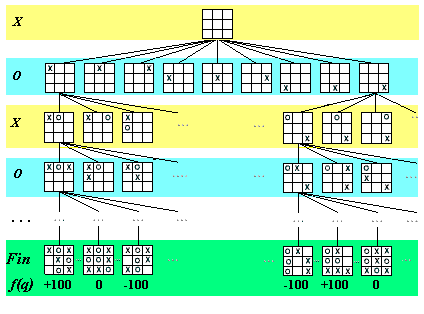
Figure 3.4.1. Présentation partielle de l`arbre de jeu pour Tic Tac Toe (dans la bande `Fin` sont
présentés des nœuds terminaux, mêmes s`ils ne sont pas tous au même niveau)

Parce que les joueurs ont droit à un seul coup, l'un après l`autre, les niveaux de décisions pour les deux joueurs alternent. En bas de la figure on trouve un rectangle vert où sont représentés tous les nœuds terminaux qi quels que soient leurs niveaux, avec les valeurs de f(qi) déterminées pour le joueur X.

Dans le cas des jeux complexes on ne peut pas construire un arbre de jeu dans sa totalité et, à cause de la limitation de l'espace mémoire et du temps de calcul, on va considérer que les nœuds situés à une profondeur P de l'arbre sont terminaux. Si le jeu n'est pas fini à cette profondeur, en réalité ces nœuds représentent des positions intermédiaires pour la partie, et une évaluation statique de ces positions ne peut pas se faire toujours sur la base de critères indiscutables : victoire, défaite ou partie nulle. C'est pour cette raison qu'on utilise souvent des critères plus ou moins objectifs. Si on prend comme l'exemple le jeu de Tic Tac Toe on peut associer à une position intermédiaire une valeur

Eval(p) = S n_i - S m_i

où n_i est le nombre des cases marquées avec X sur les lignes, colonnes et diagonales où ne se trouvent que de X (ces lignes, colonnes et diagonales représentant des occasions pour gagner) et m_i de même pour le joueur O. On observe que devant S m_i il y a le signe moins, parce qu`il s`agit des occasions gagnantes pour l`adversaire.

Question. Combien d'états sont-ils représentés dans un arbre complet pour le jeu de Tic Tac Toe de 3x3 et 4x4 ?

Cliquez ici pour voir la réponse