3. Algorithmes de recherche dans les systèmes à agents
3.4. Stratégies en jeux

3.4.2. L`algorithme MINIMAX

On va noter par MAX l'agent qu'on cherche à faire gagner et son adversaire par MIN. Les deux joueurs désirent gagner le jeu. On suppose que le joueur MIN joue logiquement et qu'il ne va jamais rater une occasion de gagner. Si pour gagner le joueur MAX essaie de maximiser son score, le joueur MIN désire aussi maximiser son propre score (ou de minimiser le score du joueur MAX).

L'algorithme MINIMAX, dû à Von Neumann, à comme but l'élaboration d'une stratégie optimale pour le joueur MAX.

À chaque tour le joueur MAX va choisir le coup qui va maximiser son score, tout en minimisant les bénéfices de l'adversaire. Ces bénéfices sont évalués en termes de la fonction d'évaluation statique utilisée pour apprécier les positions pendant le jeu.

Pour des raisons de temps de calcul et de mémoire, l'analyse est faite pour un horizon de jeu de P, le nombre de coups en avant (la profondeur de l'arbre de jeu examiné).

On a vu que l'évaluation statique des positions terminales de jeu est simple et précise : il faut apprécier selon les règles du jeu s'il s'agit d'une victoire, d'une défaite ou d'une égalité. Pour les postions intermédiaires cette fonction est imprécise, à cause des critères plus au moins subjectifs qui ont été utilisé pour l'évaluation. Le manque d'exactitude de la fonction d'évaluation statique est compensée par l'analyse rigoureuse des conséquences de chaque coup de deux joueurs.

L'algorithme réalise une évaluation de la position courante, représentée par la racine de l'arbre de jeu, en partant des nœuds terminaux. Dans ce but l'ensemble des nœuds de l'arbre de jeu est divisé en deux classes : les nœuds MAX sur les niveaux où ce joueur va choisir un coup et les nœuds MIN pour les niveaux de décision du joueur MIN.

Exemple. On considère que pendant une partie de Tic Tac Toe on est arrivé dans la position présentée dans la racine de l`arbre de la figure 3.4.2. On voit que le premier niveau est coloré en jaune, donc c'est au tour du joueur X (le joueur  MAX) de jouer.

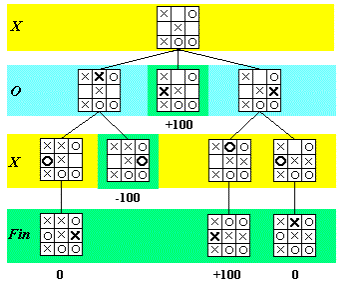
Figure 3.4.2. Exemple d`analyse pendant une partie de Tic Tac Toe

Les niveaux de décision pour le joueur MIN sont colorés en bleu et les positions terminales sont présentées dans des zones vertes, ayant écrit au-dessous les valeurs de la fonction d`évaluation statique.

L`arbre de jeu correspondant à cette position est présenté dans la figure 3.4.3. Les nœuds MAX et MIN sont représentés par des triangles. Les nœuds MIN se distinguent des nœuds MAX par la position du triangle et, en général, ils ne sont pas colorés. Mais pour garder une correspondance facile avec la situation de la figure 3.4.2 on a coloré les nœuds avec les mêmes couleurs que les niveaux de décisions des joueurs.

Sous les nœuds terminaux (soit MIN soit MAX, mais tous colorés en vert ) on a marqué la valeur de la fonction d`évaluation statique (+100 pour la victoire de MAX, 0 pour une partie nulle, et -100 pour la victoire de MIN).

L`algorithme MINIMAX associe une valeur à la racine, selon laquelle le joueur MAX fera le choix de son coup. Un algorithme pour l`agent qui implémente le joueur MAX comportera les phases suivantes :

• Construire l`arbre de jeu pour P niveaux
• Visiter l`arbre de jeu par niveaux, en montant des nœuds terminaux jusqu`à la racine:
  • si le nœud courant p représente une position terminale, on lui associe la valeur de la fonction d`évaluation statique, f(p)
• s'il s'agit d'une position intermediaire et d'un nœud MIN on lui associe la plus petite des valeurs associées à ses fils
• s'il s'agit d'une position intermediaire et d'un nœud MAX on lui associe la valeur maximale qui a été associée à ses fils
• Quand on a réussi à associer une valeur à la racine (appelée valeur MiniMax), on fait le choix de coup qui mène vers le fils qui a cette valeur maximale. S'il y a plusieurs fils qui ont la même valeur, alors on en choisit un au hasard (ou celui qui conduit à la victoire, ou celui qui conduit à une situation finale dans le plus petit nombre de coups, ou un autre critère selon les spécificités du jeu).

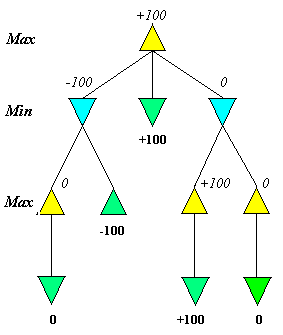
Figure 3.4.3. L`arbre MIN-MAX

Exemple. On peut voir dans la figure 3.4.3 ce processus d`association des valeurs aux nœuds intermédiaires, valeurs marquées en Italiques. La valeur MiniMax obtenue (+100) est la meilleure valeur possible à partir de la position considérée, et apporte en ce cas la victoire en un coup pour le joueur MAX,  s`il se dirige vers le fils situé au milieu en la figure. S`il fait le choix de se diriger vers le fils situé à gauche, qui a une valeur associée de –100, il va perdre la partie, si l`opposant joue de façon optimale. S `il se dirige vers le fils avec la valeur associé 0 il obtiendra un résultat nul.

La valeur MiniMax qui sera déterminée ne peut pas garantir la victoire pour le joueur MAX, mais le conduira toujours dans la meilleure situation possible pour la position donnée.

Exemple. Le jeu des allumettes. Sur une table il y a au départ quelques allumettes. Chaque joueur peut choisir à son tour de prendre 1,2 ou 3 allumettes en même temps. Le joueur qui retire la dernière allumette a perdu. L'arbre MINIMAX pour la situation avec 5 allumettes sur la table et le tour de l'agent MAX est présenté dans la figure 3.4.4, où dans les triangles sont inscrits les nombres des allumettes se trouvant sur la table avant le coup.

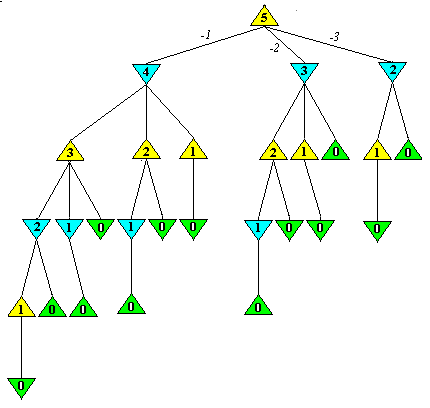
Figure 3.4.4. L`arbre MiniMax pour le jeu “des allumettes”

Les opérateurs qui modélisent les coups sont -1, -2, -3 (le nombre des allumettes qui sont pris par l'agent) et ils sont toujours appliqués dans cet ordre, de gauche à droite dans l'arbre de jeu présenté. Pour les trois premiers arcs qui partent de la position initiale, on a montré le nombre d'allumettes retirées, mais pour simplifier le dessin on ne l'a pas fait figurer sur les arcs des autres niveaux. La fonction d'évaluation statique associe à une position terminale victorieuse pour l'agent MAX la valeur +100, et -100 pour une position perdante.

Si on détermine la valeur MiniMax pour la situation avec 5 allumettes sur la table et le tour du joueur MAX, on va trouver –100, donc le joueur MAX va perdre la partie si le joueur MIN joue de façon logique. On peut observer que les valeurs associées à tous les nœuds MIN successeurs de la racine sont égales à –100, donc quel que soit l`opérateur appliqué (le coup)  par l`agent MAX, on va arriver dans une position gagnante pour le joueur MIN.

En effet, si l'agent MAX retire 1 allumette, l'agent MIN en retire à son tour 3, si MAX en retire 2, MIN en retire 2 aussi et si MAX en retire 3, MIN va en retirer 1, et dans toutes ces situations MAX va trouver sur la table 1 allumette qu'il sera forcé de prendre, donc il perdra la partie.

Questions. Considèrez le successeur direct le plus à gauche de la racine, qui correspond à une position avec 4 allumettes sur la table.

1) Quelles sont les valeurs associées à ses fils ?
2) Quelle est la valeur n (n<5) des allumettes qui peuvent être sur la table et, si c' est le tour du joueur MAX, peut-il gagner le jeu?

Cliquez ici pour voir la réponse

L`algorithme MINIMAX peut être décrit par le pseudo code suivant.

fonction MINIMAX( p) est
     maxime = -MAX_VAL
     pour *) chacune fils = successeur(p) faire
          val_fils = ValeurMINI(fils)
          si val_fils > maxime alors
               maxime = val_fils
               coup = fils
     fin pour
     retourner coup
Fin

fonction ValeurMINI ( n ) est
     si  Feuille( n )= vrai alors
          retourner f(n)
     sinon
          v_min = MAX_VAL
          pour *) chacune fils = successeur(p) faire
               v_fils = ValeurMAX(fils)
               v_min = min (v_min, v_fils)
          fin pour
     fin si 
     retourner v_min
Fin

fonction ValeurMAX ( n ) est
     si  Feuille( n )= vrai alors
          retourner f(n)
     sinon
          v_max = -MAX_VAL
          pour *) chacune fils = successeur(p) faire
               v_fils = ValeurMINI(fils)
               v_max= max(v_max,v_fils)
          fin pour
     fin si 
     retourner v_max
Fin

Les fonctions max(x,y) et min(x,y) retournent la plus grande / petite valeur de l'ensemble {x , y}. La fonction Feuille(n) retourne vrai si le nœud n est un nœud terminal (fin de jeu ou nœud terminal pour la recherche d'un arbre de jeu à profondeur limitée P).

La fonction MINIMAX appelle pour tous les fils de la racine p (la position initiale) la fonction ValeurMINI(fils) parce que tous les fils de la racine sont des nœuds MINI. On remarque une récursivité indirecte: la fonction ValeurMINI(n)appelle la fonction ValeurMAX(fils), qui à son tour appelle la fonction ValeurMINI(fils), en assurant ainsi l`alternance des traitement MINI – MAX dans l`exploration de l`arbre de jeu.

Question. Quel type d`exploration dans l`arbre de jeu réalise l`algorithme MINIMAX présenté ?

Cliquez ici pour voir la réponse

L`analyse de l`algorithme MINIMAX
Complète – oui si l`arbre de jeu est fini
Optimal – oui si le joueur MAX a un adversaire qui joue de façon optimale
Complexité en temps - O(b<sup>P</sup> )
Complexité en place – pour une exploration de l`arbre de jeu en profondeur d`abord O(bP)

Il faut préciser que pour les jeux complexes la solution exacte ne peut pas être trouvée dans un temps raisonnable. Par exemple le jeu d`échec a un facteur de branchement b=35 et pour des jeux communs P=100, donc on obtient un nombre de traitements de l`ordre 35¹⁰⁰, ce qui est un nombre géant (pour faire une comparaison, le nombre des atomes de l`univers est de l'ordre de 10¹⁰⁰). Il est nécessaire des trouver des stratégies plus pratiques.