3. Algorithmes de recherche dans les systèmes à agents
3.4. Stratégies en jeux

3.4.3. L`élagage  Alpha-Beta

On observe que l`algorithme MINIMAX effectue l`évaluation pour tous les nœuds de l`arbre de jeu d`un horizon donné. Mais il existe des situations dans lesquelles, pour déterminer la valeur MiniMax associée à la racine, il n'est pas nécessaire de calculer les valeurs associées à tous les nœuds de l'arbre. On peut remarquer une telle situation dans la figure 3.4.3, où la racine a un fils avec la valeur maximale possible (+100), donc les valeurs des autres fils n'importent pas : elles ne peuvent pas changer la valeur MiniMax

L`algorithme d`élagage Alpha-Beta conduit à une économie de temps de calcul et mémoire, en renonçant à l`évaluation des sous arbres dès que leur valeur devient inintéressante pour le calcul de la valeur associée aux nœuds père de ces sous arbres.

• Pour réaliser l`algorithme Alpha-Beta on va associer à chaque nœud n de type MAX une valeur auxiliaire appelée Alpha(n) égale à la valeur de f(n) si n est un nœud terminal, ou à la meilleur valeur de ses fils trouvée jusqu`ici;
• une valeur Beta(m) pour les nœuds MIN, valeur égale à f(m), si m est un nœud terminal, ou à la valeur minimum de ses successeurs trouvés jusqu`ici

Parce que dans un arbre de jeu les niveaux des nœuds de type MAX et MIN s`alternent, on a les relations suivantes

Alpha(n) = max {Beta(f₁), …, Beta(f_k) }

Beta(m) = min {Alpha(j₁), .. Alpha(j_k) }

Beta(f_i) <= Alpha ( Père(f_i) )

Alpha(f_i) >= Beta ( Père(f_i) )

où f_i et j_i sont respectivement les fils de n et de m

Dans l`exécution de l`algorithme Alpha-Beta coupe les sous arbres selon les règles suivantes:

• on interrompt la recherche d`un nœud n de type MAX si Alpha(n) ³ Beta(Père(n)), parce que c`est une valeur inintéressante qui ne peut pas changer la valeur Beta du nœud père de n (qui est un nœud de type MIN);
• on interrompt la recherche d`un nœud m de type MIN si  Beta(m) £ Alpha (Père(m)) parce que cette valeur ne peut pas influencer le processus de détermination du maximum qui établit la valeur Alpha de son père.

De cette façon, l`algorithme Alpha-Beta ne génère plus les successeurs d`un nœud dès qu`il est évident que, suite aux propriétés des fonctions minimum et maximum et aux valeurs associées aux nœuds déjà générés, ce nœud ne sera pas pris en compte pour le choix du coup.

L`algorithme Alpha-Beta, présenté par le pseudo code qui suit, réalise la construction de l`arbre de jeu en partant d`une position p, à l`aide de l`ensemble d`opérateurs, mais sans développer les sous arbres inintéressants.

Fonction ALPHA_BETA(p, A, B, ens_opérateurs ) est
     si Feuille(p) = vrai alors
          retourner f(p)
     fin si
     sinon
          si TypeNœud(p) = MIN alors
               Beta(p)= +MAX_VAL
               pour *) chacune op dans ens_opérateurs  faire
                    fils = successeur(p, op)
                    Val = ALPHA_BETA(fils, A, Min(B,Beta(p)))
                    Beta(p)= Min(Beta(p), Val)
                    si A >= Beta(p) alors
                         retourner Beta(p)
                    fin si
               fin pour
               retourner Beta(p)
          sinon
               Alpha(p)= -MAX_VAL
               pour *) chacune op dans ens_opérateurs  faire
                    fils = successeur(p, op)
                    Val = ALPHA_BETA(fils, Max(A,Alpha(p)), B)
                    Alpha(p) = Max(Alpha(p), Val)
                    si Alpha(p) >= B alors
                         retourner Alpha(p)
                    fin si
               fin pour
               retourner Alpha(p)
          fin si 
Fin

On a noté par f(p) la valeur de la fonction d'évaluation statique et par Alpha(p) et Beta(p) les valeurs Alpha et Beta associées aux nœuds p. Les fonctions max(x,y)et min(x,y) retournent la plus grande / plus petite valeur de {x, y}. La valeur MAX_VAL représente la plus grande valeur représentable. La fonction TypeNœud(p) retourne les constantes MIN ou MAX selon le type du nœud

Quand on appelle la fonction Alpha-Beta(p,A,B) on est sûr que A £ B.

Par sa récursivité la fonction Alpha_Beta() réalise une recherche en profondeur d'abord, en assurant une évaluation des valeurs associées aux nœuds en remontant vers la racine.

Exemple. On va suivre l'exécution de l'élagage Alpha-Beta sur l'arbre de jeu présenté dans la figure 3.4.5.

On commence avec la racine, ce qui provoque une avance en profondeur vers le fils de la racine le plus à gauche et ensuite encore un appel la fonction Alfa_Beta(p,A,B), de sorte que le premier nœud évalué est le nœud terminal dont la valeur f(p) est 12. On conclut que Beta(Père(p))<=12. Ensuite on évalue le nœud terminal ayant f(q)=7 ; il en résulte que Beta(Père(q))<=7 et après l'évaluation du troisième fils, r, on a Beta(Père(r)) = 4. On remonte à la racine et on conclut Alpha(racine) >= 4.

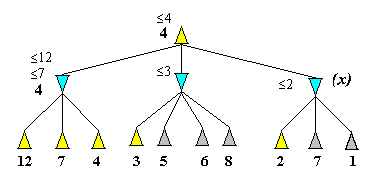
Figure 3.4.5. Exemple d`élagage alpha-beta
Les nœuds gris n`ont pas été évalués

On passe alors au deuxième fils de la racine, puis on avance en profondeur jusqu`au nœud ayant f(n)=3. On voit alors que la valeur Beta du deuxième fils de la racine est plus petite que 3. En ce cas on interrompt la recherche des trois autres fils, parce qu'on sait déjà que Alpha(racine) >= 4 et donc le deuxième sous arbre ne peut pas modifier la valeur Alpha associée à la racine.

On passe enfin au troisième fils de la racine, noté x, et on fait ensuite une nouvelle avance en profondeur en arrivant au nœud terminal ayant f(t)=2. On voit là que Beta(x) <= 2. Mais on constate que Beta(x) <= Alpha( Père(x)), parce que le père de x est la racine et on a déjà que Alpha(racine) >= 4, donc on interrompt la recherche des fils du nœud x.

à la fin, la fonction  Alpha-Beta(racine,A,B) retourne la valeur 4. Cette valeur est égale à la valeur MiniMax, mais on a évalué seulement 9 nœuds sur 14.

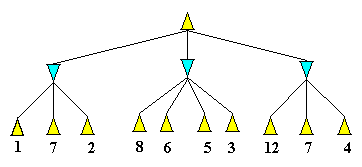
Figure 3.4.6. L`arbre de jeu de figure 3.4.5 présenté ici
avec un autre ordre préalable sur l`ensemble des opérateurs

Remarque. L`application des opérateurs dans un ordre différent conduit à un autre ordre des nœuds dans l`arbre de jeu (voir figure 3.4.6) et à des performances de recherche différentes.

Question. Combien des nœuds seront visités par l`algorithme Alpha-Beta dans le cas de l`arbre présenté sur la figure 3.4.6

Cliquez ici pour voir la réponse

Remarques

1. L'algorithme Alpha-Beta ne modifie pas le résultat final et peut accélérer le raisonnement de l'agent.
2. 2. Si on peut établir un ordre préalable sur l'ensemble des coups, alors on obtient une réduction de la complexité en temps qui peut aller jusqu'à O(b^P/2), ce qui permet à un agent qui exécute l`algorithme Alpha-Beta d`analyser un arbre de jeu d`une profondeur double de celle que peut analyser dans le même temps un agent qui implémente l`algorithme MINIMAX. Une plus grande profondeur de l`arbre de jeu recherché assure une analyse plus minutieuse des coups, donc plus de chances de gagner.

Avec un bon ordre préalable sur l'ensemble des coups l'algorithme Alpha-Beta peut assurer pour le jeu d'échec un horizon de 8 coups en avance, ce qui permet à un agent de jouer dignement à ce jeu.

Questions. Soit le jeu des allumettes et l`arbre MINIMAX présenté dans la figure 3.4.4.  

1. Combien de nœuds seront-ils évalués selon l'algorithme d'élagage Alpha-Beta en supposant que l'ordre préalable sur l'ensemble des successeurs est de gauche à droite dans la figure 3.4.4 et en tenant compte que les valeurs possibles sont comprises dans l'intervalle [-100,100] ?
2. Comment peut-on minimiser encore le nombre des nœuds étendus ?

Cliquez ici pour voir la réponse