3. Algorithmes de recherche dans les systèmes à agents
3.1. Recherche de la solution du problème
3.1.3. Algorithmes de recherche monoagent
Dans cette classe des algorithmes les plus connus sont les algorithmes
qui implémentent les suivantes stratégies:
- recherche en largeur (breadth first)
- recherche en profondeur (depth first)
- recherche en profondeur limitée
- recherche par approfondissement successif
La seule différence entre les deux premiers algorithmes est l`ordre
dans lequel se déroule l`exploration des états du problème.
La plupart des problèmes réels se déroulent dans
un espace d`états d`une complexité exponentielle ce qui
présente de sérieux obstacles dans l`application de ces
algorithmes. A cette fin les deux derniers algorithmes, constituant des
variantes des deux premiers , essaient de limiter l`explosion du nombre
d'états d`un problème réel.
Tous ces algorithmes peuvent être obtenus en partant de l`algorithme
général décrit dans la section précédente.
Recherche en largeur (breadth first)
Cette méthode de recherche explore les états d`un problème
en étendant toujours le nœud le moins profond. On peut développer
l`algorithme en utilisant dans la fonction RechercheGénéral()
une file d`attente pour la structure S. On rappelle que
les opérations avec une file d`attente se déroulent à
ses deux extrémités : l`élément qui va
être extrait le premier se trouve en tête de la file et les
successeurs du nœud visité seront introduits à la fin de
la file.
Exemple. Dans la figure 3.1.3 est présenté le graphe
représentant un espace d`états avec 7 états :
a,b, …, g, l`état initial est a et l`état solution est noté
par f.
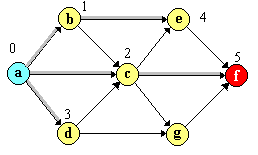
Figure 3.1.3. Parcours en largeur
d`abord
L`ordre dans lequel ont été étendus les nœuds est
précisé sur la figure par les chiffres au-dessus des nœuds,
ainsi que les opérateurs (les liens) utilisés.
Analyse de l`algorithme de recherche en largeur
Complétude – oui pour les espaces d`états finis et
acycliques
Complexité en temps – exponentielle : O(b
p) où p est la profondeur et b est le facteur de
branchement
Complexité en espace– exponentielle : O(b
p )
Optimalité - non
Remarque. Le mécanisme pour éviter les cycles infinis
basé sur l`introduction dans la structure S des seuls nœuds qui
n`ont pas été visités peut s`avérer très
difficile parce que dans certains problèmes réels la vérification
de l`identité de deux états ne peut pas être toujours
faite.
Recherche en profondeur (depth first)
Cette méthode va étendre toujours le nœud le plus profonde.
Pour réaliser l`algorithme on va utiliser pour la structure S le
TAD pile dans la fonction RechercheGénéral (étatInitial,
ens_opérateurs) présentée en 3.1.3. On se rappelle
que la stratégie d`accès aux éléments d`une
pile est “dernier entré - premier sorti”. En conséquence,
l`élément qui se trouve “en tête” de la structure
S est le dernier nœud dans l`ordre chronologique inséré
dans la pile. Donc après l`insertion des successeurs de l`état
initial on va extraire un de ces successeurs et, s`il n`est pas un état
solution, on va insérer ses propres successeurs. Quand on reprend
la boucle tant que on va analyser un de ces successeurs, même si
on n'a pas fini de traiter les successeurs de l`état initial. Donc
l`expansion des états sera faite avec priorité donnée
à la profondeur.
Exemple. Soit le même graphe que celui de figure 3.1.3.
Le résultat de recherche en profondeur d`abord, de l`état
but f est présentée dans la figure 3.1.4. On a considéré
que dans le cycle « pour *) chacune op dans
ensemble_opérateurs faire » l`ordre dans lequel sont
pris en compte les opérateurs op dans ensemble_opérateurs
est l`ordre lexicographique.
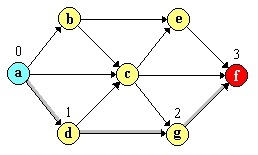
Figure 3.1.4 Parcours en profondeur
d`abord
L`exécution des traitements commence avec le nœud a. Les
successeurs de a ont été empilés dans l`ordre
b,c et d. Après le nœud a c'est le nœud d,
parce qu`il est le dernier nœud introduit dans la pile ce moment-là.
Ensuite, on introduira dans la pile les successeurs de d: c
et g . Mais Valide(c) retournera faux parce que c est déjà
dans la pile, donc seulement g sera introduit et ensuite il sera
extrait et éliminé. Le seul successeur de g est f
qui sera visité le dernier et l`algorithme s`arrêtera parce
que TestBut(f) = vrai.
Analyse de l`algorithme de recherche en profondeur
Complet pour les espaces d`états finis et acycliques
Complexité en temps – exponentielle : O(b
p) où p est la profondeur et b est le facteur de
branchement
Complexité en espace– linéaire : O(b×p)
Optimalité - non
Recherche en profondeur limitée
Pour beaucoup de problèmes réels l`espace d`états
est très complexe et d`une profondeur très grande ce qui
fait que la durée de l`algorithme de recherche en profondeur ne
peut pas avoir des performances acceptables.
L`algorithme de recherche en profondeur limitée va utiliser un
indicateur de profondeur pour les nœuds. On va considérer que tous
les nœuds situés à une profondeur plus grande qu`une valeur
limite L n`ont pas de successeurs.
Fonction RechercheEnProfondeurLimitée (étatInitial,ens_op,L)
est
S = PileVide()
Empiler (S, (Nœud(étatInitial),0))
tant que non Vide(S) faire
(NœudCourant, ProfondCourante) = Dépiler ( S )
if Test_But(NœudCourant)=vrai
alors
Détruire (S)
retourne NœudCourant
sinon
if ProfondCourante < L
alors
pour *) chacune op dans ensemble_opérateurs
faire
x = Successeur(NœudCourant,op)
si Valide(x)
alors Empiler(S,(x. ProfondCourante+1)) fin si
fin pour
fin si
fin si
fin tant que
Détruire (S)
retourne vide
Fin
Remarque. Dans la pile S on mémorise toujours des couples
(nœud, profondeur_du_ nœud). Les fonctions Empiler et Dépiler
sont appelées dans la littérature anglaise push et pop.
Analyse de l`algorithme de recherche en profondeur
Complétude – garantie si la profondeur du nœud solution
est inférieure à L
Complexité en temps – exponentielle : O(b
L) où p est la profondeur et b est le facteur de
branchement
Complexité en espace– linéaire : O(b×L)
Optimalité - non
Question. Soit un espace d`états représenté
par le graphe de figure 3.1.3 Pour quelles valeurs de la limite,
l`algorithme de recherche en profondeur limitée se termine sans
obtenir une solution?
Cliquer ici pour
voir la réponse.
Recherche par approfondissement successif
L`idée de l`algorithme c`est d`exécuter
la recherche en profondeur limitée en utilisant des valeurs croissantes
pour la limite L jusqu`à l`obtention de la solution.
Fonction RechercheApprofondSuccessif (étatInitial,ens_op)
est
pour L=0, Lmax faire
si RechercheEnProfondeurLimitée(étatInitial,ens_op,L)
<> vide
alors
retourne solution
fin si
fin pour
retourne vide
Fin
Cet algorithme combine les avantages de la
recherche en profondeur et de la recherche en largeur. Comme l`algorithme
de recherche en largeur, l`algorithme de recherche par approfondissement
successif est complet et a une complexité en espace de même
ordre que la recherche en profondeur.
Question.
Considérez un processus de recherche par approfondissement successif
dans l`espace d`états représenté par le graphe de
figure 3.1.3 . Quels sont les appeles de la fonction TestBut() lors
de l`exécution de la procédure RechercheApprofondSuccessif(a,
opérateurs ) ?
Cliquer ici pour voir
la réponse.
Un désavantage consiste dans le fait
que les nœuds situés à des profondeurs plus faibles que
le nœud solution seront visités plusieurs fois. Il en est ainsi
parce que l`exploration commence avec l`état initial pour chaque
valeur de L. D`autre part, les expansions multiples des nœuds ne concernent
pas les nœuds situés au niveau plus bas, qui sont plus nombreux
que les nœuds des niveaux supérieurs, donc le gaspillage n'est
pas très important. Malgré ce désavantage la complexité
en temps reste du même ordre que la complexité de l`algorithme
de recherche en profondeur et pour de grands espaces d`états la
recherche par approfondissement successif s`avère plus efficace
que les recherche standard en profondeur et largeur.
Question.
Queles sont les algorithmes de recherche présentés dans
cette section et quels sont les types abstraits de données de la
structure S utilisés pour obtenir ces algorithmes de l`algorithme
général de recherche présenté dans la section
3.1.2.
Cliquer ici pour voir
la réponse.
|
