3. Algorithmes de recherche dans les systèmes à agents
3.1. Recherche de la solution du problème
3.1.4. Recherche bidirectionelle
Cette stratégie peut être modélisée par l`action
de deux agents qui exécutent chacun un algorithme de recherche,
mais un agent a comme point de départ l`état initial et
le deuxième part de l`état solution et se dirige vers l`état
initial. Les agents communiquent en se transmettant leurs frontières
de recherche et le processus s`arrête quand les deux agents se rencontrent
ou quand un agent arrive à destination (l`état but pour
le premier ou l`état initial pour le deuxième).
Cet algorithme peut être appliqué seulement dans les cas
où on dispose des inverses de tous les opérateurs du problème
(e.g. les déplacements dans un labyrinthe pour trouver la sortie),
donc l`espace d`états peut être un graphe non-orienté
et on connaît l`état solution.
Exemple. Dans le même graphe que celui présenté
antérieurement se déroule un processus de recherche bidirectionnelle
effectué par deux agents.A1 et A2.
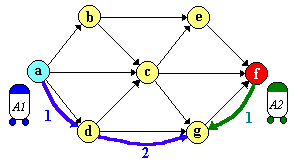
Figure 3.1.5. Recherche bidirectionnelle
effectué par deux agents.A1 (bleu) et A2 (vert)
Les agents effectuent la recherche en alternance et communiquent réciproquement
les points où ils sont arrivés. Les déplacements
de l`agent A1 ont été marqués par la couleur bleue
et ceux de l`agent A2 par la couleur verte. L`agent A2 dispose de l`inverse
des opérateurs et l`ordre de leur application (ce qui donne l`ordre
de ses successeurs) est le même que dans le cas de l`agent A1.
Analyse de l`algorithme de recherche bidirectionnelle
Complétude – oui
Complexité en temps – exponentielle : si les frontières
de recherche se rencontrent à une profondeur p/2 alors la
complexité en temps sera O(b p/2)
Complexité en espace– linéaire : O(b×p)
si les agent exécutent chacun l`algorithme de recherche en profondeur
Optimalité - non
 Question.
Soit le problème des Tours de Hanoi dans le cas particulier avec
2 disques situés sur la tour 1 et où le but est de placer
les disques sur la tour 3. Imaginez une recherche bidirectionnelle, avec
des agents qui appliquent la stratégie de recherche en profondeur
d`abord et où chaque agent applique les opérateurs mij
dans l`ordre lexicographique. Comment se terminera le processus de recherche ?
Cliquer ici pour voir
la réponse.
Remarque. Cet algorithme peut se dérouler sous une version
monoagent : on travaille avec deux piles S1 et S2, on explore à
chaque itération deux nœuds qui seront étendus si les deux
processus d`expansion d`états ne se sont pas rencontrés.
Dans cette version, si l`algorithme se termine à une profondeur
de p/2, la complexité en temps sera O(2×
b p/2), qui est meilleure que O(b p).
|
