3. Algorithmes de recherche dans les systèmes à agents
3.2. Recherche informée distribuée

3.2.1. Recherche heuristique de la solution

Les algorithmes présentés dans la section 3.1 ne peuvent pas résoudre beaucoup des problèmes réels à cause de la complexité de leurs espaces d`états.

La recherche heuristique représente alors une technique alternative de résolution de problèmes en intelligence artificielle, largement utilisée pour les problèmes qui sont caractérisés par une explosion combinatoire d`états. Alors que les algorithmes non-informés réalisent une recherche systématique et `aveugle`, les techniques de recherche heuristique utilisent un ensemble de règles qui permettent d`évaluer la probabilité qu`un chemin allant du nœud courant au nœud solution soit meilleur que les autres. Cette information qui permet l`estimation des bénéfices des divers chemins avant les parcourir améliore, dans la plupart des cas, le processus de recherche.

Les algorithmes de recherche heuristique utilisent des fonctions appelées fonctions heuristiques,

où E est l`espace d`états et R l`ensemble de réels. La valeur h(s) estime, par exemple, le rapport coût / bénéfice de suivre un chemin vers la solution qui passe par l`état s dans E. Evidemment, si le nœud s est le nœud solution alors on a la contrainte h(s)=0.

Remarque: Si h(s) = 0 sur les états solutions, c'est donc le minimum de l'heuristique que l'on recherche en chaque état.

L`idée de base d`un tel algorithme consiste dans la détermination pour chaque nœud n exploré de l`ensemble:

et de continuer la recherche avec le nœud so, tel que h(so) soit le minimum / maximum de H(n), selon l`heuristique utilisée.

Parce que les algorithmes de recherche heuristique tirent profit d`une information partielle, en dehors de l`espace d'états, ils sont appelés aussi des algorithmes informés.

L`algorithme de recherche du meilleur d`abord (Best-First Search)

Dans cette technique de recherche on étend toujours le nœud qui a la meilleure valeur h(s). Cet algorithme peut être obtenu par la particularisation de l`algorithme général de recherche présenté dans la section 3.1.1 en utilisant pour la structure S une file ordonnée.

Fonction RechercheMeilleurD_abord (étatInitial, ensemble_opérateurs, h) est

 S = FileOrdonnéVide()
 Insérer( S, (Nœud(étatInitial), 0) )
 tant que non Vide(S)  faire
      NœudCourant = Extraire ( S )
      if Test_But(NœudCourant)= vrai 
      alors
            Détruire (S)
            retourne NœudCourant
      sinon
            pour *) chacune op dans ensemble_opérateurs faire
            x = Successeur(NodeCourant,op)
            si Valide(x)
                  alors Insérer(S,x, h(x))
            fin si
            fin pour
      fin si
fin tant que
Détruire (S)
retourne vide
Fin

La fonction Insérer(S,x, h(x)) va insérer le nœud x dans la structure S, de façon que tous les éléments de S soient ordonnés dans l`ordre croissant des valeurs de la fonction heuristique  h(x).

La fonction Extraire(S) va retourner le nœud x ayant la plus petite valeur h(x) de tous les nœuds qui se trouvent en S puis cette fonction va éliminer x de S. Dans les cas où il y a un ensemble de nœuds ayant la même valeur minimum on va décider en faveur du nœud solution, s`il est contenu dans cet ensemble, sinon on choisit au hasard.

L`algorithme combine les avantages des principaux algorithmes non-informés :

• en profondeur : il cherche toujours un seul chemin, le plus prometteur selon la fonction heuristique utilisée;
• en largeur : à chaque pas il prend en considération tous les successeurs d`un nœud pour déterminer l`ensemble H(n)

Le choix de la fonction heuristique s`avère très important pour l`efficacité de la recherche effectuée par l`algorithme.

Qualité des fonctions heuristiques

L`utilité des fonctions heuristiques réside dans la limitation du nombre d'états à développer ou autrement dit, dans la diminution de branchements effectués pendant la recherche, ce qui conduit à une économie de temps et d`espace mémoire.

Pour évaluer la qualité d`une fonction heuristique on peut calculer le facteur de branchement effectif qui est une valeur a posteriori du processus de recherche. Soit N le nombre d`états explorés pendant un processus de recherche de la solution d`un problème concret en utilisant une fonction heuristique h() et  soit P la profondeur du nœud solution dans ce processus de recherche. Pour calculer la valeur du facteur de branchement effective b<sub>e</sub>  on considère un arbre fictif, parfaitement équilibré ayant le branchement b<sub>e</sub> dont le nombre de nœuds peut être calculé par l`équation 

N = 1 + b_e + b_e² + … + b_e^P

et N, le nombre d`états explorés, doit être égal au nombre de nœuds dans cet arbre fictif.

Une heuristique de bonne qualité aura la valeur du facteur de branchement effective b_e très proche de 1. Dans le cas idéal, où on trouve la solution sans étendre d'autres nœuds que ceux situés sur le chemin entre l`état initial et la solution, on a b_e =1. 

Il existe plusieurs méthodes de recherche heuristiques.

La recherche gourmande (Greedy Search)

Cette technique représente la plus simple variante de la stratégie de recherche le meilleur d`abord (Best Search). Pour construire l`algorithme de recherche gourmande on modifie l`algorithme RechercheMeilleurD_abord, mais en utilisant une fonction heuristique h(n) qui estime le coût du chemin entre le nœud courant et le nœud solution. La fonction Insérer(S,x, h(x)) va insérer le nœud x dans la structure S, de façon que tous les éléments de S soient ordonnés dans l`ordre croissant des valeurs de la fonction heuristique h(x). La fonction Extraire(S) va donc retourner et va éliminer de S le nœud le plus proche du nœud solution.

Analyse de l`algorithme de recherche gourmande (Greedy Search)
Complétude – NON, on peut rester pris dans une boucle ; il peut être complet  pour les espaces d`états finis et acycliques
Complexité en temps – exponentielle : O(b ^p) où p est la profondeur et b est le facteur de branchement
Complexité en  espace – exponentielle : O(b ^p )
Optimalité - NON

Avec des bonnes heuristiques on peut avoir des complexités en temps meilleures.

La recherche en coût uniforme (Uniform Cost Search)

Cet algorithme utilise une heuristique qui calcule pour chaque nœud n le coût chemin g(n) depuis l`état initial jusqu'au nœud n. Le coût chemin g(n) est une fonction croissante le long d`un chemin : chacune n dans E, s dans Successeurs(n),   g(n) <= g(s).

Les nœuds sont insérés dans la file ordonnée S dans l`ordre croissant de la fonction g(n), de façon qu`à chaque itération le nœud qui minimise g(n) soit développé pour obtenir ainsi un chemin de coût minimum entre l `état initial et la solution.

L`algorithme est complet et optimal, mais a une efficacité réduite.

Programmation dynamique asynchrone. La recherche du plus court chemin

On considère un graphe orienté où les nœuds correspondent aux états du problème. Il y a un nœud de départ s et plusieurs nœuds but. Entre les nœuds existent des liens représentant les opérateurs qui sont appliqués aux états du problème.

Les poids des liens sont considerés comme des distances. Soit d(i,j) la distance entre les nœuds i et j. Le problème de la recherche du plus court chemin exige de trouver le chemin de coût minimum (exprimé à l`aide des distances) entre le nœud s et un nœud but.

La programmation dynamique est basée sur le principe d`optimalité qui affirme qu`un chemin est optimal si tous ces ses sous chemins le sont.

Pour évaluer le coût d`un chemin qui part d'un nœud i et va jusqu`à un nœud but il faut évaluer les coûts de tous les chemins qui partent de i et passent par les nœuds j, successeurs de i:

f*(j) = d(i,j) + h*(j)

où h*(j) est la distance la plus courte de i jusqu'à un nœud but. On aura h*(i) = min { f*(j) / chacune j dans Successeurs(i)}.

Un algorithme de programmation dynamique utilise le principe d`optimalité pour construire pas à pas le chemin vers la solution en étendant des sous chemins de longueur croissante, qui sont tous optimaux.

Algorithme de programmation dynamique asynchrone

La programmation dynamique asynchrone représente une technique de recherche distribuée basée sur un réseaux d`agents. Pour chaque nœud i du graphe modélisant l`espace d`états on a un agent A_i qui va calculer en mode répété h(i), une estimation de h*(i). Tous les agents connaissent les successeurs j et les distances d(i,j) entre le nœud courant i et ses successeurs, ainsi que les valeurs initiales de h(i) qui sont égales à la valeur maximale admise (VAL_MAX) pour tous les agents sauf les agents des nœuds but qui ont h(i)=h*(i)=0.

Chaque agent A_i exécute en principe des traitements selon le pseudo code suivant et détermine le nœud successeur jmin(i), afin que le principe d`optimalité soit respecté.

pour *) chacune op dans ensemble_opérateurs, avec op valide faire
      j = Successeur(i,op)
      f(j) = d(i,j) + h(j)
      si h(i) > f(j)
            alors
            h(i)=f(j)
            jmin(i) = j
      fin si
fin pour

Le chemin sera représenté par le chaîne : s, jmin(s), jmin( jmin(s) ) , … , but

Remarque. Le chaîne h(i) converge vers h*(i) parce que les distances d(i,j) sont positives.

Pour les problèmes réels la technique présente le désavantage de nécessiter un très grand nombre des agents.

L`algorithme A*

Cet algorithme est aussi un cas particulier de l`algorithme de recherche du meilleur d`abord. Il combine les avantages des algorithmes de recherche en coût uniforme et de recherche gourmande (Greedy Search), en utilisant une heuristique f()

f(n) = g(n) + h(n)

où n est un nœud représentant un état dans l`espace d`états du problème et g(n) et h(n) ont les significations utilisées dans le cas de ces deux algorithmes. Cette heuristique estime le coût total du chemin entre l`état initial et l`état solution qui passe par n. On remarque qu`il s`agit d`une estimation f(n) obtenue par la somme d`une valeur exacte g(n) issue du chemin parcouru de l`état initial jusqu`au nœud n et d`une estimation h(n) du coût du chemin optimal qui lie le nœud n avec au nœud solution.

Pour chaque nœud exploré n on va étendre le successeur x qui minimise la fonction heuristique f()

f(x) = min { f(s) / s dans Successeurs( n )  }

Définition. Une fonction heuristique est dite admissible si

h(s) <=h*(s), chacune s dans E

où h*(s) est le coût minimum depuis s au nœud solution.

Analyse de l`algorithme de recherche A*
Complet pour les espaces d`états avec du coût du chemin optimal qui relie le nœud n au nœud solution s ayant f(s)<=f(but)
Complexité en temps – exponentielle
Complexité en  espace– exponentielle
Optimalité – l`algorithme A* est optimal ; il étend toujours les nœuds dans l`ordre croissant de valeurs heuristiques ; l`optimalité de l`algorithme A* est garantie si on utilise une heuristique admissible

Remarques

1. On observe que l`algorithme A* peut être construit sur la base de l`algorithme de recherche du meilleur d`abord (Best First Search) en utilisant une fonction heuristique égale à la somme du coût calculé pour arriver dans le nœud n et du coût estimé pour atteindre un état solution. Si la fonction qui estime le coût nécessaire pour atteindre un état but ne surévalue jamais le coût réel, alors l`algorithme A* est optimal.
2. Il arrive que l'on ait à choisir parmi plusieurs fonctions heuristiques admissibles. Un critère est fourni ci-dessous:

Soit deux fonctions heuristiques admissibles h₁(s) et h₂(s). Si

h₁(s) >= h₂(s), chacune s dans E

on dit alors que h₁(s) domine h₂(s) et que h₁(s) produit une recherche plus efficace.

Exemple. On considère un jeu de Taquin 3x3 (voir figure 3.2.1).

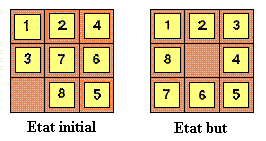
Figure 3.2.1. L`état initial et final dans un jeu de Taquin

à chaque état du jeu on peut appliquer des opérateurs qui permettent de déplacer les pièces voisines de la position libre. Le but de jeu de Taquin est de trouver une séquence optimale d'opérateurs qui mène les pièces de la configuration de l'état initial à l'état but.

 On peut considérer deux heuristiques :

• h1(i) exprimé comme le nombre des pièces mal placées dans l`état i
• h2(i) calculé comme la somme des distances Manhattan entre la position dans l`état i et la position dans l`état final de chaque pièce.

Pour les états représentés dans la figure 3.2.1 on a

h₁(s) = 5
h₂(s) = 0 + 0 +3 + 1 + 0 +2 + 2  + 2 = 10

On observe que h₂(s) > h₁(s). Si cette inégalité est valable pour tous les états on peut dire que h₂(s) est une heuristique dominante.

Les heuristiques dominantes sont préférées tant qu`elles ne surestiment pas le coût minimum.

Question. Quel sera l`état suivant, selon l`algorithme A* appliqué pour la situation présentée dans la figure 3.2.1, en considérant l`heuristique dominante h₂(x) ?

Cliquer ici pour voir la réponse

Variantes de l`algorithme A*

La recherche de la solution des problèmes concrets se confronte avec des espaces d`états très grands, qui soulèvent des difficultés majeures en termes d`espace de mémoire nécessaire, même dans le cas des algorithmes heuristiques.

Deux variantes de l`algorithme A* essaient d`aboutir à une solution avec les ressources disponibles :

• IDA* (Iterated-Depending A*) qui est un algorithme A* qui effectue des approfondissements successifs en rapport avec des valeurs limites pour f(n) ; IDA* est complète et optimale et sa complexité en espace mémoire est de l`ordre O(b×p)
• SMA* (Simplified Memory-Bounded A*) qui est un algorithme A* qui effectue la gestion de sa propre mémoire disponible: élimine les nœuds ayant les valeurs de f(n) plus élevées quand la file ordonnée est pleine. L`algorithme SMA* est complet si l`espace mémoire disponible est suffisant pour contenir le chemin état initial – état solution. L`algorithme SMA* retourne toujours la meilleure solution qui peut être obtenue avec l`espace mémoire alloué.