3. Algorithmes de recherche dans les systèmes à agents
3.1. Recherche de la solution du problème
3.2.2. Recherche en temps réel de but fixe ou de cible mobile
On peut imaginer par exemple un agent qui contrôle les déplacements
d`un robot vers une destination finale. Dans le processus de recherche
en temps réel (Real Time Search) de sa destination, on va déterminer
à chaque pas la position suivante la plus plausible et ensuite
on va effectuer le déplacement. En ce mode, le chemin vers la solution
sera construit pas à pas, pendant le déplacement physique
du robot.
Remarque. Dans le cas des algorithmes off-line présentés
dans la section 3.1, l`agent de recherche détermine premièrement
le chemin entier vers le point final et puis va donner toutes les
commandes nécessaires pour que le robot arrive à la destination.
La recherche en temps réel s'avère très efficace
dans des situations incertaines ou dans des environnements dynamiques
(on se rend compte facilement de l'échec des algorithmes off-line
si dans le champ d'action du robot un obstacle change sa position après
la détermination du chemin). Il existe d'autres situations qui
réclament la recherche en temps réel : par exemple, les
cas où les senseurs du robot sont limités en espace et le
robot "ne voit pas" le point final, ce qui l'empêche,
au moins lorsqu'il est au point initial, d'établir une trajectoire
vers sa destination.
Dans la formalisation des algorithmes de recherche en temps réel
on va considérer que l`espace d`états est représenté
par un graphe non-orienté connexe. On ne dispose pas d`une carte
représentant le graphe entier, mais d`une heuristique admissible
qui estime le coût du chemin vers un nœud but (pour les nœuds but
on a toujours h(but)=0). Pour simplifier la présentation
on suppose que tous les arcs ont un coût égal à 1.
Chaque itération exécutée par les algorithmes de
recherche en temps réel dans le processus de recherche possède
deux phases :
- la détermination du mouvement suivant qui va placer l'agent
dans un état successeur et
- l'exécution de ce mouvement (on va supposer aussi que tous
les mouvements ont la même durée).
Dans la recherche en temps réel existent deux types de problèmes
selon la mobilité du but:
- des problèmes caractérisés par une position fixe
du but pendant la recherche (Fixed Goal Problem)
- des problèmes où la position du but peut changer -
cible mouvante (Moving Target Problem).
Remarque. La recherche off-line ne peut traiter que le problème
de but fixe.
Recherche en temps réel de but fixe (Fixed Goal Problem)
Les algorithmes de recherche de but fixe les plus connus sont les suivants :
En principe les deux algorithmes comportent à chaque itération
les deux phases parcourues par les algorithmes de recherche:
- on détermine le mouvement suivant
- on exécute en temps constant ce mouvement.
Pour déterminer le mouvement on a besoin des distances vers le
but. Initialement toutes les distances sont estimées à l`aide
de la fonction heuristique. Dans le cas des problèmes réels
le calcul de h(n) pour tous les nœuds est très coûteux,
donc on adopte une stratégie dans laquelle le calcul des valeurs
heuristiques est restreint aux nœuds étendus. Pendant l`exploration
de l`espace d`états les distances prennent des valeurs plus précises,
à la suite de l`apprentissage.
Dans ce qui suit on va noter par n le nœud courant et par h(n)
la valeur courante d`heuristique qui estime la distance jusqu`au nœud
but.
Apprentissage A* en temps réel (LRTA* - Learning Real Time
A*)
L`algorithme LRTA* détermine et apprend les nouvelles valeurs
de h(n) à chaque itération selon la fonction suivante.
Fonction DétermineSuivant_LRTA(n, h ,ens_opérateurs)
est
H = Ø
pour *) chacune op dans ens_opérateurs,
avec op valide faire
s = Successeur(n,op)
*) calculer h(s)
H = H è {h(s)}
fin pour
*) soit sm le nœud ayant h(sm) = min ( H )
retourne sm
Fin
On va actualiser h(n) avec la valeur h(sm) plus 1, parce
qu`on a supposé que le coût de tout arc est égal à
1. En général on peut actualiser : h(n)=h(sm) +
coût(n,sm).
Le processus global de recherche en temps réel peut être
représenté par la procédure suivante :
Procédure Agent_LRTA_étoile (étatInitial,
h ,ens_opérateurs) est
NœudCourant = Nœud(étatInitial)
tant que Test_But(NœudCourant)=faux faire
NœudSuivant=DétermineSuivant_LRTA(NœudCourant, h,
ens_opérateurs)
h(NœudCourant) = h (NœudSuivant) + 1
ExécuteMouvement(NœudCourant,NœudSuivant)
NœudCourant = NœudSuivant
fin tant que
Fin
La procédure ExécuteMouvement(NœudCourant,NœudSuivant)
réalise le déplacement physique de l`agent vers une nouvelle
position. On se rappelle que la complexité de cette fonction est
supposée O(1). L`agent réalise aussi
la mise à jour des valeurs heuristiques des nœuds explorés
(les NœudCourants) .
Analyse de l`algorithme de recherche LRTA*
Complétude – garantie pour les espaces d`états finis,
si les arcs ont des coûts positifs il existe un chemin depuis chaque nœud
vers le but et on part avec des valeurs non- négatives pour h(n)
Optimalité – OUI si l`algorithme utilise une heuristique
admissible
Remarques
- Parce que les valeurs h(n) = h(sm) + 1 représentent
des limites inférieures pour les distances de chemins depuis
n vers le but en passant par les successeurs de n, alors
les nouvelles valeurs gardent l`admissibilité de h(n).
- Les valeurs apprises par LRTA* peuvent converger vers les valeurs
exactes de chaque chemin optimal vers la solution.
L`algorithme A* en temps réel ( Real Time A* ou RTA* )
L`algorithme ressemble bien à l`algorithme LRTA* à l`exception
de la mise à jour de h(n) pendant l`exploration de l`espace
d`états
Fonction DétermineSuivant_RTA(n, h ,ens_opérateurs)
est
H = Ø
pour *) chacune op dans ens_opérateurs,
avec op valide faire
s = Successeur(n,op)
*) calculer h(s)
H = H U {h(s)}
fin pour
*) soit sm le nœud ayant h(sm) = deuxième_min(H)
retourne sm
Fin
La nouvelle valeur de h(n) sera évidemment h(n) = h(sm) + 1,
où sm est le nœud successeur de n qui a la deuxième
valeur dans l'ordre croissant des valeurs des h(s) lorsque
s parcourt les nœuds successeurs de n. Cette actualisation
sera faite dans une procédure Agent_RTA_étoile presqu'identique
à la procédure Agent_LRTA_étoile.
La fonction deuxième_min, appelée dans la fonction DétermineSuivant_RTA
choisit donc la deuxième meilleure valeur pour h(n).
L`analyse des performances de LRTA* reste valable pour RTA* avec
les remarques suivantes:
- l`algorithme RTA* s`avère plus rapide que LRTA* ;
- RTA* présente le risque de surestimer les distances heuristiques
et de faire un nombre d`opérations de recherche plus grand.
Recherche de cible mouvante (Moving Target Search - MTS)
Dans cette classe de problèmes, pendant le processus de recherche
le but change sa position à travers des nœuds du graphe représentant
l`espace d`états. Suite à ces changements les valeurs de
la fonction heuristique peuvent se modifier. Dans ce qui suit le nœud
but sera appelé cible.
On va supposer que l`agent de recherche et la cible changent leurs positions
successivement, dans un des successeurs des nœuds où on se trouve.
La fonction heuristique h : ExE -> R prendra
en compte les positions de l`agent et de la cible. On doit avoir donc
une matrice h(x,y), où x est la position de l`agent
et y la position de la cible. En pratique on retient seulement
les valeurs h(x,y) qui ne sont pas égales aux valeurs initiales.
La vitesse de la cible est supposée plus faible que la vitesse
de l`agent de recherche (dans certaines situations l`agent exécute
un mouvement, mais la cible reste dans la même position). On suppose
aussi que l`agent de recherche connaît toujours la position y de
la cible.
L`algorithme MTS est basé sur LRTA* et ne surestime jamais les
distances heuristiques.
 Question.
Pourquoi s'intéresse-t-on aux heuristiques admissibles, qui ne
surestiment jamais le vrai coût minimum h*(x) ? Question.
Pourquoi s'intéresse-t-on aux heuristiques admissibles, qui ne
surestiment jamais le vrai coût minimum h*(x) ?
Procédure Agent_MTS (étatInitial, h ,ens_opérateurs)
est
x = Nœud(étatInitial)
y = PositionBut()
tant que x ¹ y faire
NœudSuivant=DétermineSuivant_MTS (NœudCourant, y,
h, ens_opérateurs)
h (x,y) = max { h(NœudSuivant,y)+1 , h(x,y)}
ExécuteMouvement (NœudCourant,NœudSuivant)
x = NœudSuivant
y = ObserveCible(x,y,h)
fin tant que
FinLa fonction suivante reçoit comme argument la référence
de h, considérée comme matrice. On va supposer alors
que les modifications sur h(x,y), faites localement sont transmises
à l' extérieur et sont donc accessibles aux autres fonctions.
Fonction ObserveCible(x, y, h) est
ynouveau = PositionBut()
si y <> ynouveau alors
*) calculer h(x,ynouveau) pour la nouvelle pos. de la cible
h (x,y) = max { h(x,ynouveau)-1 , h(x,y)}
y = ynouveau
fin si
retourne y
Fin
On remarque que dans le cas d`un mouvement de la cible on diminue la
valeur de 1, parce qu`on se rappelle qu`on a supposé que tous les
mouvements sont au plus de la longueur d`un arc, dont le coût est 1.
La fonction DétermineSuivant_MTS() est en fait la fonction DétermineSuivant_LRTA(),
transformée en tenant compte de la position y de la cible.
Fonction DétermineSuivant_MTS(x,y, h ,ens_opérateurs)
est
hmin = VAL_MAX
pour *) chacune op dans ens_opérateurs,
avec op valide faire
s = Successeur(x,op)
*) calculer h(s,y)
si hmin > h(s,y) alors
hmin = h(s,y)
sm = s
fin si
fin pour
retourne sm
Fin
L`algorithme de recherche de cible mouvante (MTS) est complet dans
le sens qu`il atteint la cible si :
- périodiquement la cible ne change pas de position (sa vitesse
est plus faible que celle de l`agent de recherche),
- l'espace d'états est fini, sans cycles, il existe un chemin
entre chaque couple de nœuds et
- les valeurs initiales de h(x,y) sont non-négatives et admissibles.
La procédure Agent_MTS() représente en fait une généralisation
de l`algorithme de recherche Agent_LRTA_étoile() présenté
pour la recherche de but fixe. On peut observer facilement que si la fonction
ObserveCible() ne détecte aucune mouvement de la cible, les traitements
exécutés par cette fonction dans le cas de l`Agent_MTS()
sont identiques que pour Agent_LRTA_étoile()
Performances des algorithmes de recherche en temps réel (RTR)
Il paraît évident que les performances des algorithmes de recherche
en temps réel dépendent fortement de la topographie de l`espace
d `états estimé. à la base de cette affirmation
se trouve le fait que chaque mouvement de l`agent de recherche ou / et
de la cible a une forte influence sur le processus de recherche qui se
déroule après le déplacement. On peut expliquer le
comportement des algorithmes RTR par une nouvelle notion.
Définition. On appelle dépression heuristique
un ensemble d`états connectés, ayant les valeurs heuristiques
égales ou plus petites que les valeurs des états qui les
entourent complet et direct.
Définition. Une dépression heuristique est dite
maximale locale si aucun des états qui entourent complet et direct
la dépression heuristique ne peut être ajouté à
la dépression.
On peut se rendre compte facillement sur ces notions en regardant l'exemple
qui suit.
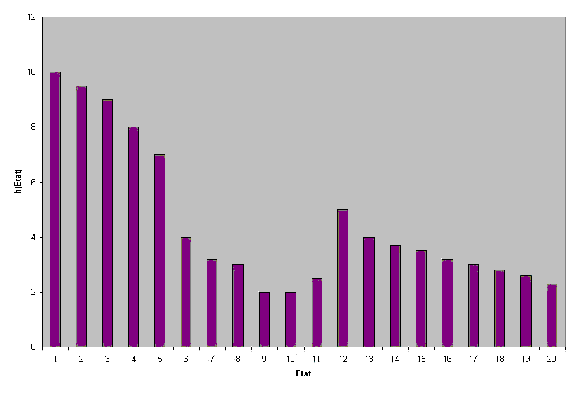
Figure 3.2.2. Exemple d`une heuristique dans un espace d`états
à 20 états
Exemple:. On considère le cas d'un espace d'états
unidimensionnel présenté dans la figure 3.2.2, où
les états sont identifiés par des nombre entiers de 1 à
20 et chaque état s a deux successeurs identifiés par s-1
et s+1. On peut y observer une dépression heuristique formée
par les états 9 et 10, parce que ces états ont des valeurs
heuristiques plus petite que les états 8 et 11 qui les entourent
direct et complet. Si on ajoute l'état 11 on obtient une nouvelle
dépression {9,10,11}. La dépression heuristique maximale
locale est D={6,7,8,9,10,11} parce que si on ajoute soit l'état
5, soit l'état 12, l'ensemble D n'est pas une dépression
heuristique.
Si l'heuristique est basée sur une distance, il ne peut pas y
avoir de dépressions heuristiques dans les valeurs initiales, mais
des dépressions peuvent apparaître pendant le processus de
recherche.
Si une décision erronée est prise à la frontière
d'une dépression heuristique, l 'agent de recherche arrive dans
le fond de la dépression. Pour en sortir, il faut qu'il effectue
des itérations supplémentaires pour augmenter la valeur
heuristique des états appartenant à la dépression.
On peut affirmer que l'agent ne peut sortir d'une dépression qu'après
"le remplissage de la dépression " en exécutant
h(NœudCourant) = h (NœudSuivant) + 1 (algorithme LRTA* ou RTA*)
ou
h (x,y) = max { h(NœudSuivant,y)+1 , h(x,y)} (algorithme MTS).
selon l`algorithme de recherche implémenté par l`agent.
Ces processus de " remplissage de la dépression " ralentissent
notablement l'exécution de l'algorithme de recherche. La fonction
heuristique utilisée pour la recherche et sa topographie influencent
dans une grande mesure les performances de l'algorithme de recherche.
 Question.
Soit un espace d`états à 7 états, dont a est
l`état initial et f est le but Question.
Soit un espace d`états à 7 états, dont a est
l`état initial et f est le but

et soit les valeurs initiales de l`heuristique h(a)=5, h(b)=4, h(c)=1,
h(d)=1, h(e)=3 h(f)=0. Quelles sont à la fin de la recherche
les valeurs de l`heuristique?
Exemple. Dans le cas d`un labyrinthe la topographie d`une dépression
heuristique est présenté dans la figure 3.2.3.
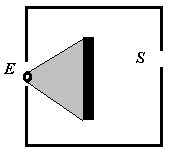
Figure 3.2.3. Exemple de topographie
heuristique
En face de l`agent qui se trouve à l`entrée et doit aller
à la sortie (S) existe un mur. La région grisée représente
la dépression heuristique maximale locale.
Les performances des techniques de recherche en temps réel dépendent
très fortement de la topographie de l`heuristique, qui inclut l`espace
du problème et les valeurs heuristiques.
|

